 Уводът на Ландау
Уводът на Ландау
Никъде не съм срещал толкова красиво и силно изложение, както в курса по теоретична физика
под ръководството на Л. Д. Ландау.
Написаното тук е преразказ на част от уводните текстове в том 3.
Има връзка с предни статии:
Оператори,
Материални вълни,
Уравнение на Шрьодингер.
Собствени Пси-функции
Нека f е физична величина с дискретно множество от собствени стойности
 .
.
Да означим с
 вълновата функция, описваща такова състояние, при което измерването на f ще даде стойност
вълновата функция, описваща такова състояние, при което измерването на f ще даде стойност
 .
.
Съгласно принципът на суперпозицията - дефиниран в статията "Оператори",
 - функцията може да се представи като линейна комбинация от
- функцията може да се представи като линейна комбинация от
 - функции, съответствуващи на
- функции, съответствуващи на  - стойностите:
- стойностите:
 , [1]
, [1]
където an са някакви коефициенти.
Така, всяка Пси-функция може да се разложи
на множество функции  по коя да е физична величина f - наричани Собствени Пси функции.
по коя да е физична величина f - наричани Собствени Пси функции.
Горният сбор [1] дава възможност да оценим каква е вероятността за резултат fn при измерването на f.
От статията "оператори", равенство [3] знаем, че вероятността е
линейна по  , също и по
, също и по  .
Двата равностойни множителя под знака за сума от [1] показват, че тя е билинейна и по a-коефициентите.
Тази вероятност е реално положително число - единица, когато
.
Двата равностойни множителя под знака за сума от [1] показват, че тя е билинейна и по a-коефициентите.
Тази вероятност е реално положително число - единица, когато
 съвпада с
съвпада с  и нула във всички останали случаи. Такова число може да бъде само
и нула във всички останали случаи. Такова число може да бъде само
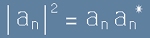 [2].
[2].
Тоест a-коефициентите изразяват вероятностно разпределение. В такъв случай, те трябва да имат сбор единица:
 [3].
[3].
- точно както и Пси функцията. С други думи е вярно следното равенство:
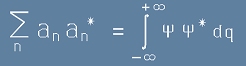 [4].
[4].
Сега да обърнем внимание на комплексно-спрегнатата Пси-функция. За нея важи аналогично на [1] равенство:
 [5].
[5].
Да умножим двете страни на това равенство с Пси:
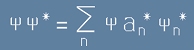 [6]
[6]
и да интегрираме по цялото q-пространство. Ще получим:
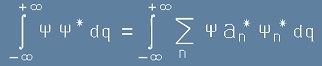 . [7]
. [7]
Да съпоставим [7] и [4]. Вижда се, че
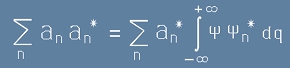 [8]
[8]
и така получихме израз за a-коефициентите:
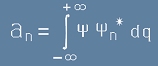 . [9]
. [9]
Да заместим [1] в [9]:
 . [10]
. [10]
Щом е вярно горното равенство [10], то със сигурност можем да твърдим, че
 , [11]
, [11]
или, казано с думи собствените функции образуват ортонормирано множество.
Средни стойности и оператори
Имайки от по-горе (равенство [2]) представа за вероятностния характер на а-коефициентите, можем да дефинираме
по естествен начин средното на величината f. По уговорка средната стойност се означава с
хоризонтална черта над буквата и представлява сбор:
 . [12]
. [12]
[Отклонение 1]
Да умножим равенството [1] с комплексно-спрегнатата Пси функция и да интегрираме по цялото пространство:
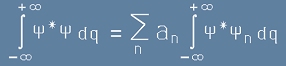 . [13]
. [13]
Да препишем условието за нормировка от [4] по-горе като
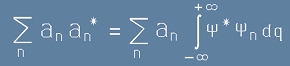 . [14]
. [14]
Така получихме израз за комплексно-спрегнатите a-коефициенти:
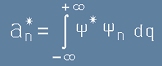 . [15]
. [15]
[/Край на Отклонение 1]
Да заместим [15] в [12}:
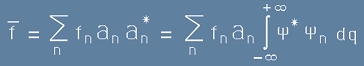 . [16]
. [16]
или по-кратко:
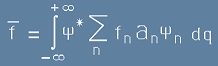 . [17]
. [17]
Сега да дефинираме оператора  като спазащ условието:
като спазащ условието:
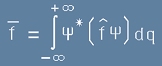 . [18]
. [18]
Съпоставката на последните две показва какво точно е действието на оператора
 над Пси-функцията:
над Пси-функцията:
 . [19]
. [19]
[Отклонение 2]
Да заместим тук a-коефициентите според [9] :
 [20]
[20]
(с изместена интегрална променлива q' за да не се смеси с основния аргумент q). Да изолираме функцията:
 [21]
[21]
- тя се нарича ядро на оператора. С това действието от [19] се записва като:
 [22]
[22]
[/Край на Отклонение 2]
Ако в [19]  съвпада с някоя собствена функция, съответния a-коефициент ще е равен
на едно а всички останали ще са нулеви и тогава то ще има вид:
съвпада с някоя собствена функция, съответния a-коефициент ще е равен
на едно а всички останали ще са нулеви и тогава то ще има вид:
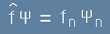 . [23]
. [23]
След всичко това може да се твърди, че собствените функции за коя да е физична величина f са решения на
уравнението:
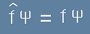 . [24]
. [24]
Радостин Желязков 15.06.2012
________________________________________________________________________________________
коментари
учебни статии по физика
 Уводът на Ландау
Уводът на Ландау
 .
. вълновата функция, описваща такова състояние, при което измерването на f ще даде стойност
вълновата функция, описваща такова състояние, при което измерването на f ще даде стойност
 .
. - функцията може да се представи като линейна комбинация от
- функцията може да се представи като линейна комбинация от
 - функции, съответствуващи на
- функции, съответствуващи на  - стойностите:
- стойностите: , [1]
, [1]  по коя да е физична величина f - наричани Собствени Пси функции.
по коя да е физична величина f - наричани Собствени Пси функции.  , също и по
, също и по  .
Двата равностойни множителя под знака за сума от [1] показват, че тя е билинейна и по a-коефициентите.
Тази вероятност е реално положително число - единица, когато
.
Двата равностойни множителя под знака за сума от [1] показват, че тя е билинейна и по a-коефициентите.
Тази вероятност е реално положително число - единица, когато
 съвпада с
съвпада с  и нула във всички останали случаи. Такова число може да бъде само
и нула във всички останали случаи. Такова число може да бъде само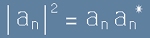 [2].
[2]. [3].
[3].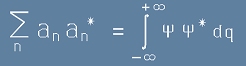 [4].
[4]. [5].
[5]. [6]
[6]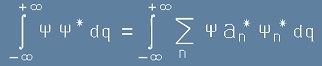 . [7]
. [7]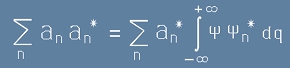 [8]
[8]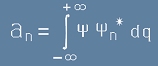 . [9]
. [9] . [10]
. [10] , [11]
, [11] . [12]
. [12]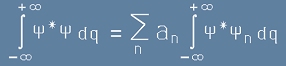 . [13]
. [13]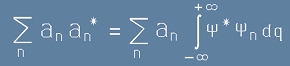 . [14]
. [14] . [15]
. [15]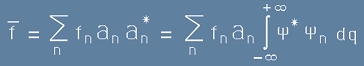 . [16]
. [16] . [17]
. [17] като спазащ условието:
като спазащ условието: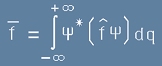 . [18]
. [18] над Пси-функцията:
над Пси-функцията: . [19]
. [19] [20]
[20] [21]
[21] [22]
[22] съвпада с някоя собствена функция, съответния a-коефициент ще е равен
на едно а всички останали ще са нулеви и тогава то ще има вид:
съвпада с някоя собствена функция, съответния a-коефициент ще е равен
на едно а всички останали ще са нулеви и тогава то ще има вид: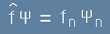 . [23]
. [23]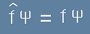 . [24]
. [24]