 Оператори
Оператори
В тази статия са обобщени тълкувания от време, значително по-късно
от момента на създаване на квантовата механика.
Тук са ползувани предни статии:
Материални вълни,
Неопределеност на Хайзенберг,
Уравнение на Шрьодингер.
След предните няколко статии навлязохме по-дълбоко в предмета и е добре е да потърсим ред в квантово-механичните представи.
В квантовата механика са възприети дефинитивно няколко принципа и основни положения.
Ще ги изброим накратко - някои от тях са вече познати по един или друг начин.
Принцип за неопределеността
Отсъствието на траектория и координатно-импулсната неопределеност вече са коментирани
в предни статии Материални вълни и
Неопределеност на Хайзенберг.
Измерването винаги променя квантово механичния обект.
Онова което нашите сетива виждат също е резултат от взаимодействието между
квантовите обекти и заобикалящата ги среда, тоест така нареченото "измерване" съществува винаги.
Принципно, в квантовата механика се предполага, че макро-класическите променливи
не просто се регистрират, а СЕ ПОЯВЯВАТ като резултат на същото това "измерване" - с определена вероятност.
С други думи, при взаимодействието (или измерването), с някаква вероятност се поражда стойност за измерваната променлива.
В този смисъл наличието и стойността на класически параметри е гарантирано само по вероятностен начин.
Задачата на квантовата механика е да пресметне именно тези вероятности.
Важна особеност при измерванията е, че не винаги всички променливи са определени.
Примери за това са двойките импулс-координата и време-енергия.
Затова понякога се говори за набор едновременно измерими променливи.
Принцип за съответствието
В граничните случаи, когато размерите, точностите и явленията клонят към класическите,
резултатите получени по квантово-механичен подход, трябва да клонят към тези, които
дава класическата физика.
Пси-функцията
Нека означим с буква q съвкупността от всички координати на квантово-механичната система.
Състоянието на системата в един момент се определя от една комплексна функция на координатите
 .
.
При това произведението
 е вероятност координатата q да заема стойности в промеждутъка dq.
е вероятност координатата q да заема стойности в промеждутъка dq.
Така, че квадрата на модула на тази функция
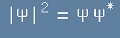 [1]
[1]
представлява вероятностното разпределение на координатата q.
Очевидно то трябва да е нормирано, тоест
 . [2]
. [2]
Пси-функцията се нарича още вълнова функция. Чрез вълновата функция се получават вероятностни изрази
за стойността на физичните променливи. Тези изрази имат интегрален вид :
 , [3]
, [3]
при което функцията фи =
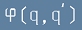 [4]
[4]
зависи от конкретната променлива.
Ако например положим
 , [5]
, [5]
(за Делта функцията на Дирак виж
[11] от статията "Уравнение на Поасон"
),
то подинтегралната функция от [3] ще се приравни точно към [1] около координатна стойност q0.
Ако в интеграла [3] заменим Пси-функцията с друга от вида
 , [6]
, [6]
където алфа е реално число, то интегралът [3] няма да се промени.
Значи Пси-функцията е свободна до множителя  , [7]
, [7]
наричан понякога фазов множител. Фазовата неопределеност на Пси-функцията е неизбежна,
но тя не влияе на физичните променливи, тъй като интегралът от [3] ще има една и съща стойност.
Най-често Пси функцията зависи не само от координатите, но и от
Времето
Ако приемем, че Пси напълно определя статуса в някакъв начален момент и знаем зависимостта от времето
 ,
,
то състоянието - пак чрез Пси-функцията, във всички бъдещи моменти от време е също определено.
Един пример за подобна зависимост вече е даден в статията
Уравнение на Шрьодингер, равенство [11]. Но както е отбелязано по-горе,
да не забравяме, че променливите са определени по статистически (вероятностен начин).
Принцип за суперпозицията
Практически, в една предна статия
Материални вълни, равенство [17] ние вече използувахме този принцип.
Формално той може да бъде изразен чрез следното твърдение:
Нека функцията
 описва такова състояние, че при измерване на някаква променлива, се получава резултат 1.
описва такова състояние, че при измерване на някаква променлива, се получава резултат 1.
Нека функцията
 описва друго състояние - такова, че при измерване на същата променлива, се получава резултат 2.
описва друго състояние - такова, че при измерване на същата променлива, се получава резултат 2.
Тогава всяка линейна комбинация
 (c1 и c2 са някакви коефициенти),
(c1 и c2 са някакви коефициенти),
описва състояние, при което измерването на тази променлива, води или до резултат 1, или до резултат 2.
Ако една система е съставена от две части, напълно описани от функциите
 и
и  ,
,
то цялата система е също напълно описана (обратното, разбира се, не е вярно - ако знаем описващата функция за цялата система,
това не е достатъчно за да опишем нейните части).
Нека при измерване на координатата q1 в първата част - описвана от
 - се получава с известна вероятност стойност Q1,
- се получава с известна вероятност стойност Q1,
а във втората част - описвана от
 -
се получава - с друга вероятност - стойност Q2.
-
се получава - с друга вероятност - стойност Q2.
В такъв случай, можем да твърдим, че вероятността първата координата да има стойност Q1
И заедно с това втората координата да има стойност Q2, е произведение от двете вероятности.
Това значи, че вълновата функция за съставната система е
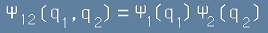 .
.
Собствени стойности
В класическата физика, най-често физичните величини са от непрекъснато множество стойности - както реалните числа.
В квантовата механика се приема, че физичните величини могат да приемат само някой стойности, наречени
техни собствени стойности.
Собствените стойности може да са от непрекъснато множество - наречено непрекъснат спектър.
Но това не винаги е така и често собствените стойности образуват дискретно множество или дискретен спектър.
Оператори
Да разгледаме производната
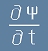 .
Може да се каже, че това е резултат от действието
на диференциален оператор
.
Може да се каже, че това е резултат от действието
на диференциален оператор
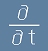 върху функцията
върху функцията
 .
.
По подобен начин произведението AF може да се разглежда като резултат от действието на умножаващ оператор A върху функцията F.
Формално казано, квантово-механичните оператори са линейни, тоест
1. Ако F и G са две функции и ако c1 и c2 са някакви константи,
A(c1F+c2G)=c1(AF)+c2(AG)
.
2. Aко A B са два оператора, C=c1A+c2B е трети оператор, такъв, че
((c1A)+(c2B))F = CF
.
Последното е възможно само при условие, че A B са едновременно измерими физични величини.
Последователното прилагане на два оператора A B е еквивалент на прилагането на трети оператор C,
наричан произведение на двата: C=AB.
Произведението не е комутативно и ако F е някаква функция, то има вид
CF=(AB)F=A(BF)
.
Една физична величина е съответна на резултат от действие на съответен оператор върху Пси-функцията.
Да си спомним
уравнението на Шрьодингер
за свободна частица и да го напишем във вида:
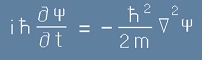 . [7]
. [7]
Сега да дефинираме два оператора:
Оператор на енергията
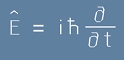 и
Оператор на импулса
и
Оператор на импулса
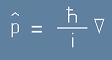 [8]
[8]
(шапка над буква ще означава оператор).
В такъв случай по-горното равенство [7] ще е еквивалент на отношение между оператори:
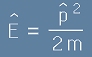 , [9]
, [9]
което е съответно на изходния класически израз за енергията, възприет в
статията за Шрьодингер, равенство [7].
Радостин Желязков 04.11.2011
________________________________________________________________________________________
коментари
учебни статии по физика
 Оператори
Оператори
 .
. е вероятност координатата q да заема стойности в промеждутъка dq.
е вероятност координатата q да заема стойности в промеждутъка dq.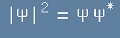 [1]
[1]  . [2]
. [2]  , [3]
, [3] [4]
[4] , [5]
, [5] , [6]
, [6] , [7]
, [7] ,
, описва такова състояние, че при измерване на някаква променлива, се получава резултат 1.
описва такова състояние, че при измерване на някаква променлива, се получава резултат 1. описва друго състояние - такова, че при измерване на същата променлива, се получава резултат 2.
описва друго състояние - такова, че при измерване на същата променлива, се получава резултат 2. (c1 и c2 са някакви коефициенти),
(c1 и c2 са някакви коефициенти),  и
и  ,
, - се получава с известна вероятност стойност Q1,
- се получава с известна вероятност стойност Q1, -
се получава - с друга вероятност - стойност Q2.
-
се получава - с друга вероятност - стойност Q2. 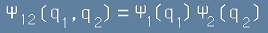 .
.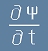 .
Може да се каже, че това е резултат от действието
на диференциален оператор
.
Може да се каже, че това е резултат от действието
на диференциален оператор
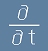 върху функцията
върху функцията
 .
.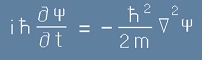 . [7]
. [7]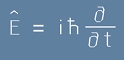 и
Оператор на импулса
и
Оператор на импулса
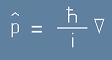 [8]
[8]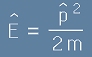 , [9]
, [9]