 Уравнение на Клайн-Гордън
Уравнение на Клайн-Гордън
Тук е изведено с обикновени средства едно уравнение, което се смята за важно в Релативистката Квантова Теория.
Ползувани са предни статии:
Материя,
Уравнение на Шрьодингер,
Оператори.
В този раздел, "Квантова физика", макар и негласно, се придържаме към нерелативисткия модел.
Тук обаче е разгледан случай, в който ограничаващото условие за класическия израз
за енергията
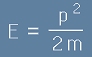 , [1]
, [1]
е заменено с друго - съгласувано с Теорията на Относителността.
Двете равенства, изразяващи енергията и импулса
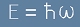 и
и
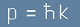 [2]
[2]
са верни и в
Релативистичен случай
Постановката за вълновата функция
 [3]
[3]
може и да варира като тълкуване от релативистична гледна точка,
но засега ще се въздържим от това и ще я смятаме за валидна .
Да пресметнем двете втори производни на [3]
- по координатата :
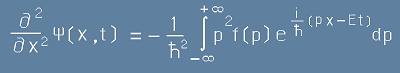 [4]
[4]
- и по времето:
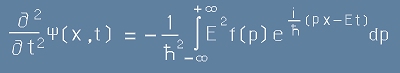 . [5]
. [5]
Съгласно релативистката теория
(виж
равенство [8.5] от статията "Материя"
),
квадратът на енергията под интеграла [5] трябва да е:
 . [6]
. [6]
Да заместим това в [5]:
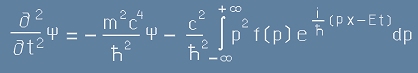 . [7]
. [7]
Вторият член от дясната страна на [7] може да бъде изразен чрез [4] :
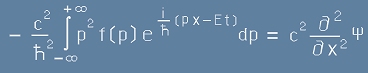 , [8]
, [8]
и така вместо [7] остава
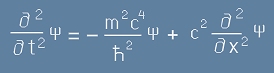 . [9]
. [9]
Последното, разделено на c2 дава едномерна версия на обещаното
Уравнение на Клайн-Гордън
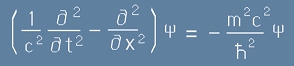 . [10]
. [10]
С операторни означения и 3D-производна, то изглежда като
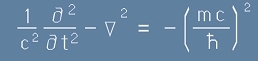 . [11]
. [11]
Радостин Желязков 05.11.2011
________________________________________________________________________________________
коментари
учебни статии по физика
 Уравнение на Клайн-Гордън
Уравнение на Клайн-Гордън
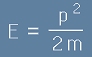 , [1]
, [1]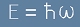 и
и
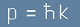 [2]
[2] [3]
[3]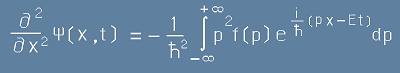 [4]
[4]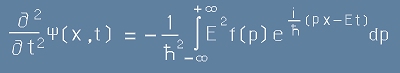 . [5]
. [5] . [6]
. [6]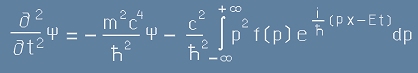 . [7]
. [7]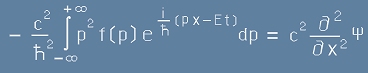 , [8]
, [8]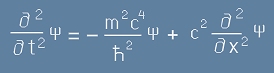 . [9]
. [9]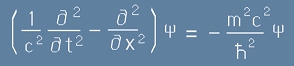 . [10]
. [10]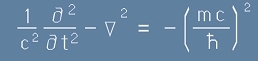 . [11]
. [11]