 Електричен потенциал
Електричен потенциал
Това е част от класическата електромагнитна теория.
Изведена е формулата за електростатичен (електричен) потенциал - като решение на Уравнението на Поасон.
Трябва да сте запознати със статиите:
Набла операции,
Уравнения на Максуел,
Уравнение на Поасон.
Електричното поле
тоест силата, действуваща на единица заряд, се изразява чрез Закона на Кулон (1783):
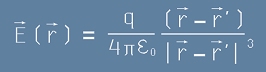 , [1]
, [1]
където E е полето, епислон е Диелектричната Проницаемост на вакуума,
r - радиус вектора на точката, за която се отнася полето,
r' - радиус вектора на точката, в която се намира заряда-източник q.
Зарядът q може да се представи като интеграл по цялото пространство, чрез функцията плътност (ро):
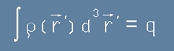 .
.
(d3r' означава елементарен обем dr'x dr'y dr'z)
И в непрекъснатия случай полето е
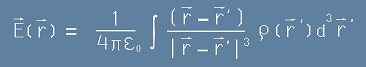 . [1.1]
. [1.1]
Да си спомним за Делта-Функцията на Дирак - [11] от статията Уравнение на Поасон.
С помощта на такава функция, зарядът q, който се намира в точка r', може да се представи чрез друг аргумент r:
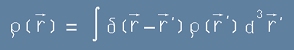 . [2]
. [2]
Да напишем първото уравнение на Максуел:
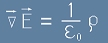 [3]
[3]
и да заместим в него горните две формули [1.1] и [2] - за полето E и за плътността на заряда ро:
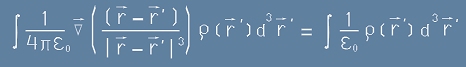 , или без интегралните знаци
, или без интегралните знаци
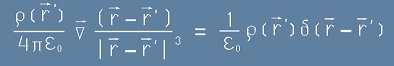 . [4]
. [4]
[Отклонение]
Да обърнем внимание на следната частна производна:
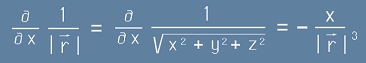 . [5]
. [5]
Тя представлява първата компонента на набла-операция върху скалара 1/r.
Никак не е трудно да си представим другите две компоненти на резултата
от същата тази набла операция и да схванем, че
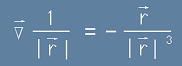 , или в контекста на [4] :
, или в контекста на [4] :
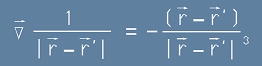 . [5.1]
. [5.1]
Набла по r към двете страни от това равенство [5.1] ще ни даде заместващ израз за набла-операцията от по-горното равенство [4] :
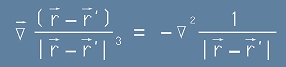 . [6]
. [6]
[/Край на отклонението]
Да заместим [6] в [4]. Ще получим уравнението
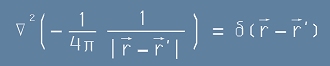 , [7]
, [7]
което е точен аналог на
равенство [13] от статията Уравнение на Поасон:
От тук разбираме две неща. Първо - описаното по-горе е пряко свързано с
Уравнението на Поасон
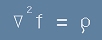 , [8]
, [8]
чието решение е потенциал f около източника ро.
Второ, от [7], веднага се вижда, че функцията на Грийн, продуцираща решения на Поасоновото уравнение трябва да е
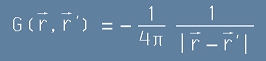 . [9]
. [9]
Да заместим тази функция във формулата за решението на Поасоновото уравнение - виж
[14] от статията Уравнение на Поасон. Получаваме
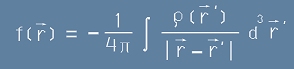 . [10]
. [10]
Електричен потенциал
Функцията f от [10] е решение на общия вид на Поасоновото уравнение [8].
Конкретното уравнение на Поасон за електричното поле е
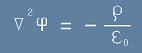 . [11]
. [11]
То е получено от [8] чрез умножение по физична константа за размерност.
Щом е така, според свойството суперпозиция, решението му ще е функцията f от [10], умножена по същата константа:
 , [12]
, [12]
Точният вид на тази функция, според [10] е
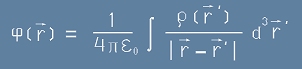 . [13]
. [13]
и се нарича още Електричен потенциал (понякога Кулонов потенциал).
Полето е градиент
Тъй като интегралната променлива в [13] е r' а не r, лесно се вижда, че градиентът на [13] по r е
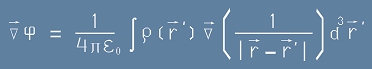 . [14]
. [14]
Имайки предвид [5.1], стигаме равенството
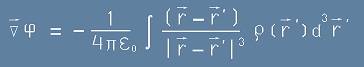 . [15]
. [15]
Да сравним дясната страна на това равенство с формула [1.1]. Това е минус Кулоновата сила.
Следователно градиентът на електричния потенциал, със знак минус, е равен на електричното поле:
 . [16]
. [16]
коментари
Радостин Желязков 31.05.2011
________________________________________________________________________________________
учебни статии по физика
 Електричен потенциал
Електричен потенциал
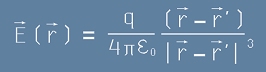 , [1]
, [1]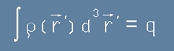 .
.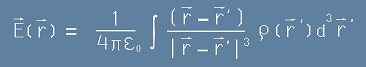 . [1.1]
. [1.1]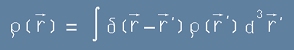 . [2]
. [2]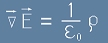 [3]
[3]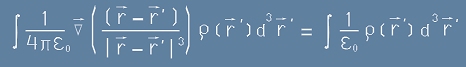 , или без интегралните знаци
, или без интегралните знаци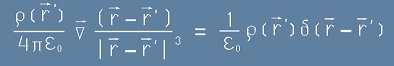 . [4]
. [4]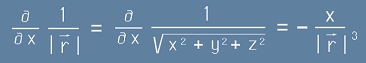 . [5]
. [5]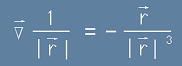 , или в контекста на [4] :
, или в контекста на [4] :
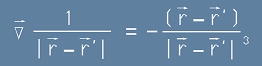 . [5.1]
. [5.1]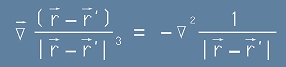 . [6]
. [6]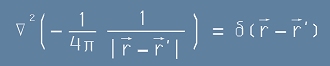 , [7]
, [7]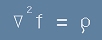 , [8]
, [8]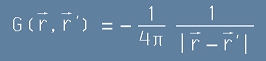 . [9]
. [9]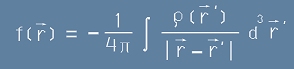 . [10]
. [10]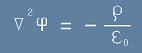 . [11]
. [11] , [12]
, [12]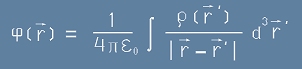 . [13]
. [13]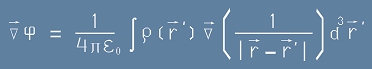 . [14]
. [14]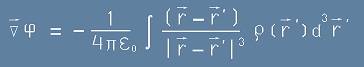 . [15]
. [15] . [16]
. [16]