 Теорема на Хелмхолц
Теорема на Хелмхолц
Това е помощна статия свързана с класическата електродинамика.
Тук са използувани знания от статиите
Набла-операции,
Уравнения на Максуел,
Уравнение на Поасон,
Електричен потенциал.
Твърдение
Теоремата на Хелмхолц гласи, че всяко векторно поле, което изчезва на безкрайно разстояние, може да бъде представено като сбор
(суперпозиция) от едно чисто дивергентно и едно чисто ротационно поле.
Това е еквивалент на твърдение, че
полето е напълно определено от своята дивергенция и ротация.
Например Уравненията на Максуел напълно описват електромагнитните вектори B и E
и тези уравнения са две двойки - за всеки от двата вектора B и E има по едно за
дивергенцията и едно за ротацията.
Илюстрация
За статични заряди и постоянни токове Уравненията на Максуел изглеждат по следния начин (производните по времето са нулеви):
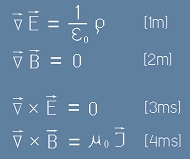 .
.
Нека F е буквата, с която означаваме полето.
"Чисто дивергентно" значи поле, за което ротацията е нула (rot F=0);
"Чисто ротационно" значи поле с нулева дивергениця (div F=0).
Горните четири уравнения са пример за едно чисто дивергентно поле (rot E = 0)
и едно чисто ротационно поле (div B = 0).
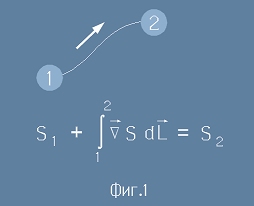
Градиентно поле
Това е векторно поле, получено чрез набла-производна от друго, скаларно поле.
В статията Електричен потенциал, равенсто [16] видяхме, че
Електростатичното поле е градиент на скаларно поле-потенциала. Тази връзка е двупосочна.
Ако знаем градиента на едно скаларно поле, самото скаларно поле е напълно определено. Ето защо:
Нека в точка 1 скаларното поле S има стойност S1. В точка 2 полето ще има стойност S2, която
може да бъде получена като сбор от S1 и интегрирания градиент по някакъв път от точка 1 до точка 2 - (фиг.1).
Следователно градиентът (grad S) носи цялата информация за скаларното поле.
Градиентът е векторно поле с нулева ротация, тъй векторното произведение между успоредни вектори
дава нулев резултат. Такъв тип поле се нарича още консервативно.
Доказателство
Нека F е векторно поле и ние знаем неговата дивергения и ротация.
Да означим като D дивергенциата на F (D е скалар) и като C ротацията на F (C е вектор):
 , [1]
, [1]
 . [2]
. [2]
Теоремата твърди, че F може да се представи като сбор от две други полета,
от които първото има само дивергенция, а второто само ротация.
Да предположим, че има скаларно поле S и векторно поле Q - такива, че
 . [3]
. [3]
В него първото събираемо е градиентно поле (тоест с нулева ротация),
а второто е чисто ротационно поле (тъй като дивергенция от ротация е нула - виж тъждество 1 от статията Набла-операции).
Да заместим [3] в [1]. Ще получим израз за дивергенциятя на F:
 , [4]
, [4]
но второто събираемо в нея е нула, така, че комбинацията на [4] с [1] води до равенството:
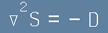 . [5]
. [5]
Това е Поасоново уравнение, за което отлично знаем, че има решение, което може да бъде намерено чрез [14] от
статията Уравнение на Поасон.
Да опитаме ротацията на вектора F от [3]. Това е сбор
 [6]
[6]
в който първото събираемо е нула, защото е ротация на градиентно поле (виж по-горе).
Да заместим [6] в [2]. Ще получим равенството
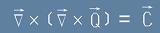 , [7]
, [7]
което е двойно векторно произведение. По правилото A x (B x C) = B(AC)-C(AB) то се свежда до
 . [8]
. [8]
Сега внимание - ще допуснем, че Q е бездивергентно поле
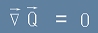 , [9] ( ! ! ! )
, [9] ( ! ! ! )
тоест, че първото събираемо от [8] е нула!
За момента такова допускане е необосновано, дори изглежда прекалено, но след малко ще покажем, че то има смисъл.
В такъв случай, от [8] остава равенството
 . [10]
. [10]
Разгледано като векторна тройка, то е еквивалент на следните три:
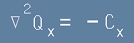 , [11]
, [11]
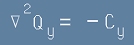 , [12]
, [12]
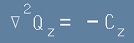 . [13]
. [13]
Те изглеждат по еднакъв начин, затова ще разгледаме подробно само първото от тях.
Очевидно това е Поасоново уравнение. Да построим неговото решение -
по аналогия с [10] от статията Електричен потенциал.
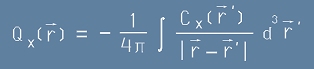 . [14]
. [14]
Да пресметнем градиента на [14]
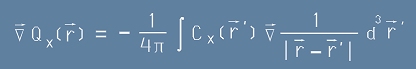 . [15]
. [15]
[Отклонение 1]
Да обърнем внимание, че
 , [16]
, [16]
където примовата набла е производна по примовата версия на r.
Освен това, ако в [15] наблата беше примова, разширеният запис за произведението вътре в интеграла би бил от типа:
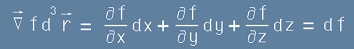 . [17]
. [17]
Като имаме предвид [16] и [17], вместо [15] от по-горе, може да се запише (това е внасяне под знака на диференциала)
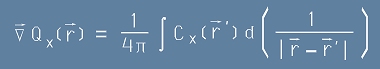 , [18]
, [18]
[/Край на отклонение 1]
[Отклонение 2]
Сега ще направим едно ценно за момента обобщение.
За какви да са две скаларни функции f g ,според правилото за интегриране по части, важи равенството:
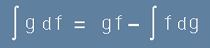 , или
, или
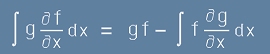 . [19]
. [19]
така, че формулата за интегриране по части с набла-производна е
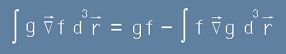 , [20]
, [20]
[/Край на отклонение 2]
Имайки предвид [20] и [18], получаваме:
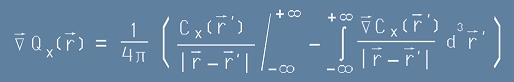 . [21]
. [21]
Тъй като в безкрайност полето F изчезва (тоест изчезват дивергенциата и ротацията му), според [2], първото събираемо в скобите е нула.
Да се върнем към векторния вид на горното равенство:
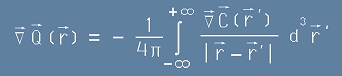 . [22]
. [22]
Но според [2], дивергенцията на вектора C също трябва да е нулева (винаги div rot=0).
От тук виждаме, че векторът Q действително има нулева дивергенция, тоест допускането [9] е съвсем разумно.
Процедурата по избора на полето Q e известна като калибровка и е предмет на специално разглеждане в следващи статии.
С това показахме, че постройката [3] е достъпна чрез решенията на четири Поасонови уравнения
[8], [11], [12], [13] - съставящи скалара S и вектора Q.
Но ако ние можем да посочим полетата Q и S от постройката [3],
това доказва и самото твърдение на Хелмхолц,
тъй като по-горе видяхме, че първото събираемо от [3] е
чисто дивергентно, а второто - чисто ротационно поле.
коментари
Радостин Желязков 04.06.2011
________________________________________________________________________________________
учебни статии по физика
 Теорема на Хелмхолц
Теорема на Хелмхолц
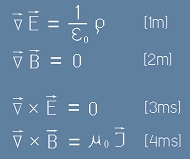 .
.
 , [1]
, [1] . [2]
. [2] . [3]
. [3] , [4]
, [4]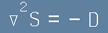 . [5]
. [5] [6]
[6]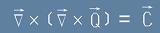 , [7]
, [7] . [8]
. [8]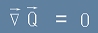 , [9] ( ! ! ! )
, [9] ( ! ! ! ) . [10]
. [10]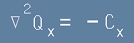 , [11]
, [11]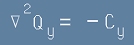 , [12]
, [12]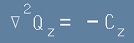 . [13]
. [13]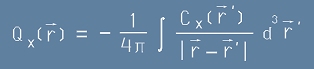 . [14]
. [14]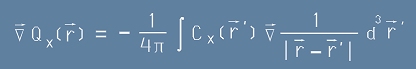 . [15]
. [15] , [16]
, [16]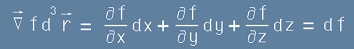 . [17]
. [17]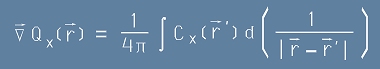 , [18]
, [18]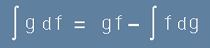 , или
, или
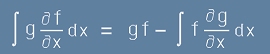 . [19]
. [19]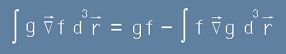 , [20]
, [20]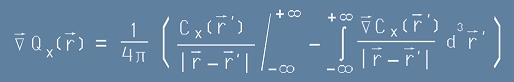 . [21]
. [21] . [22]
. [22]