 Магнитен потенциал
Магнитен потенциал
Това е част от класическата електродинамика.
Дадени са дефиниции за Магнитен и Електромагнитен потенциал, също за Калибровъчна инвариантност.
Тук са използувани знания от статиите
Векторно произведение,
Набла-операции,
Уравнения на Максуел,
Уравнение на Поасон,
Електричен потенциал.
Теорема на Хелмхолц.
Третото уравнение на Максуел:
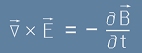 [3m]
[3m]
казва, че ротацията на вектора E не е нулева и следователно електричното поле изобщо не може да се третира
като чисто дивергентен вектор.
Такава особеност не съществува за вектора B, тъй като
Магнитното поле
е изцяло ротационно: Второто уравнение на Максуел
 [2m]
[2m]
е винаги вярно.
Според теоремата на Хелмхолц (виж едноименната статия, равенство [3]),
ако едно векторно поле B е чисто ротационно, може да се представи като ротация на друго
векторно поле A
 . [1]
. [1]
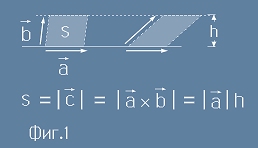 В това равенство [1], векторното поле A служи само за извличане на ротационното поле B.
В това равенство [1], векторното поле A служи само за извличане на ротационното поле B.
Различни вектори A от дясно на [1] могат да доведат до един и същ резултат B.
Да разгледаме ротацията като векторно произведение c=a x b (Виж Фиг.1). Дължината на получения вектор
е равна на лицето s на успоредника, образуван от двата вектора. Но има начин единият от тези два вектора a b да варира
- по посока и големина - при което успоредника може да запазва едно и също лице.
За по-лесно разбиране на дефиницията, можем да предположим временно, че A е чисто ротационен вектор.
Обаче ако div A не е нула, това не е пречка да бъде възможно равенството [1].
В тази статия по-долу, а и в следващи, има обсъждане на въпроса дали A e чисто ротационно поле, или не.
От начина, по който се доказва Теоремата на Хелмхолц - в условията на подобно предположение,
се вижда, че компонентите на полето A заемат мястото на потенциал в три Поасонови уравнения.
Виж равенства [2], [11], [12], [13] от Хелмхолц.
Затова векторното поле A от [1] обикновено се нарича
Магнитен Потенциал
Да заменим [1] в [3m]:
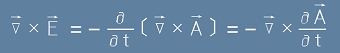 , или по-ктарко:
, или по-ктарко:
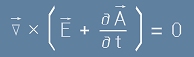 , [2]
, [2]
което показва, че в скобите на [2] се намира векторно поле с нулева ротация - чисто дивергентно поле.
Чисто дивергентните полета винаги са градиент на скаларен потенциал. Тоест съществува скаларна функция Ф, за която е вярно равенството
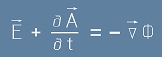 . [3]
. [3]
В такъв случай E-вектора може да се представи като
 . [4]
. [4]
Равенството [4] е винаги вярно. Електричното поле при статични заряди и токове е консервативно и се описва от скаларния потенциал Ф.
В условията на променящо се магнитно поле, векторното поле Е не е консервативно,
но се описва с добавка към скаларния потенциал - чрез вектора на магнитния потенциал A.
Четворката, образувана от скаларния потенциал Ф и трите компоненти на магнитния потенциал A
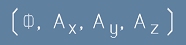 [5]
[5]
понякога се нарича
Електромагнитен потенциал
С негова помощ двата вектора - електричния и магнитния се изразяват като:
 [=4]
[=4]
 [=1] .
[=1] .
Но горните две уравнения допускат нееднозначност.
Да вземем за пример [4]. Дивергенцията е производна и отляво ще получим един и същ вектор E,
ако към Ф-скалара прибавим каква да е константа Ф0 :
 [6] .
[6] .
Подобна нееднозанчност има и при магнитния потенциал A.
Както беше показано по-горе (фиг.1), възможно е две различни векторни полета в позиция A
да доведат до една и съща стойност за B. Ето обяснение: Да направим замяната
 [7] ,
[7] ,
където пси е скаларно поле. Градиентната прибавка в [7] няма да промени ротацията от [1], защото
ротация от градиент винаги е нула.
Заедно с това, при подходящ подбор на пси-скалара, полето A може да бъде чисто ротационно.
Ето как: Условието за чисто ротационен вектор A е нулева дивергенция:
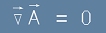 [8] .
[8] .
Ако заменим [7] в лявата страна на [8], тя ще изглежда като
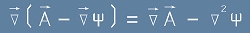 [9] .
[9] .
Но ако поискаме дясната страна на [9] да е нула, ще получим Поасоново уравнение, което
винаги има решение. Това решение би било подходящото скаларно поле, означено по-горе като пси.
Условието за чисто ротационен магнитен потенциал от [8] по-горе, е подходящо за описване на
статични полета и е известно като
Кулонова калибровка
или условие на Кулон за електромагнитния потенциал.
При това формулите за скаларния - Ф и векторния - A потенциали се получават като решения
на Поасоновите уравнения
 , [10]
, [10]
 . [11]
. [11]
Решенията са:
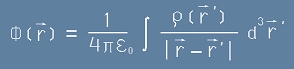 [10.1]
[10.1]
 [11.1]
[11.1]
Тези две формули описват електромагнитния потенциал [5] при статични заряди и постоянни токове.
Но Кулоновата калибровка не е единствена възможност.
Свойството на векторите B и E да се запазват при различни стойности на електромагнитния потенциал [5]
се нарича
Калибровъчна инвариантност
Константата Ф0 от [6] не променя E - вектора, защото набла-операцията [4] върху нея дава нулев резултат.
Но нулев градиент би имала и линейна функция от времето f=Ф0t.
Да прибавим тази функция към скаларното поле пси от [7] :
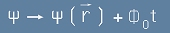 [12] .
[12] .
Тогава свободата в компонентите на електромагнитния потенциал се изразява изцяло с функцията пси от координатие и времето:
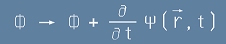 [13]
[13]
 [14]
[14]
Последните две [13] и [14] понякога се наричат калибровъчни преобразувания.
Всъщност каква да е подмяна на електромагнитните компоненти от [5], която води до
едни и същи стойности за векторните полета B и E от [1] и [4], е калибровъчно преобразувание.
коментари
Радостин Желязков 06.06.2011
________________________________________________________________________________________
учебни статии по физика
 Магнитен потенциал
Магнитен потенциал
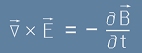 [3m]
[3m] [2m]
[2m] . [1]
. [1]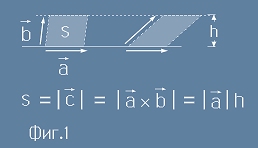 В това равенство [1], векторното поле A служи само за извличане на ротационното поле B.
В това равенство [1], векторното поле A служи само за извличане на ротационното поле B.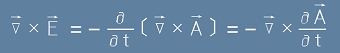 , или по-ктарко:
, или по-ктарко: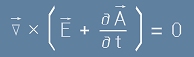 , [2]
, [2]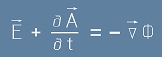 . [3]
. [3] . [4]
. [4]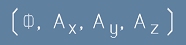 [5]
[5]  [=4]
[=4] [=1] .
[=1] . [6] .
[6] . [7] ,
[7] ,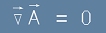 [8] .
[8] .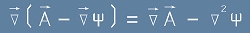 [9] .
[9] . , [10]
, [10] . [11]
. [11]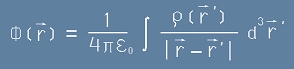 [10.1]
[10.1] [11.1]
[11.1]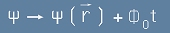 [12] .
[12] .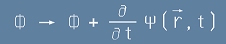 [13]
[13]  [14]
[14]