 Закъсняващи потенциали
Закъсняващи потенциали
Това е част от класическата електродинамика.
Тук са използувани знания от статиите
Набла-операции,
Уравнения на Максуел,
Уравнение на Поасон,
Електричен потенциал,
Магнитен потенциал.
Лоренцова калибровка.
В статията "Поасон", равенство [13], е казано, че
Функцията на Грийн
е решение на Поасоновото уравнение за точков заряд.
В друга статия - "Електричен потенциал", равенство [9] беше определено, че тази функция - G(r,r') - има вид:
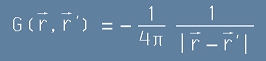 . [9p]
. [9p]
Това по методиката от Поасон породи решение за потенциалите - виж "Магнитен потенциал", равенство [10.1] и [11.1]:
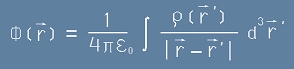 [10.1mp]
[10.1mp]
 [11.1mp]
[11.1mp]
Но тези две равенства се отнасят за постоянен заряд - тоест поле, което не се променя с времето.
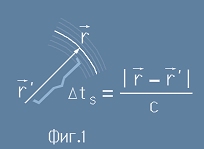
Да разгледаме поле, създавано от заряд в точка r'.
Ако наблюдател се намира в друга точка r, можем да кажем, че всяка промяна в полето
пристига със закъснение в точка r - значи след време  (виж Фиг.1).
(виж Фиг.1).
От тук идва необходимост
Да разграничим времето
 на източника t' от времето, в което наблюдателя вижда полето t.
на източника t' от времето, в което наблюдателя вижда полето t.
Ако зарядът в точка r' е функция на времето t', а полето в точка r е функция на времето t, то
начинът да укажем, че полето в момент t е предизвикано от промяна в момент t' е
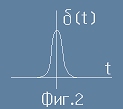
познатата ни от статията "Поасон"
делта-функция на Дирак, но с аргумент време (Фиг.2).
Делта-функцията е вид разпределение и е достатъчно да умножим [9p]
по делта, за да получим подходяща функция на Грийн, която е ненулева само в един миг
 . [1]
. [1]
Такава функция - вече ще зависи от двойка координати (r, r') и двойка времена (t,t'):
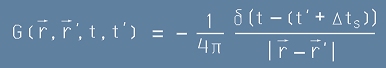 . [2]
. [2]
Разликата между G-функцията от [2] и по-горната от [9p] е, че в [9p] разглеждаме статично поле,
а явлението от последното равенство [2]
е сферичен вълнов фронт, възникнал в момент t' по временната скала на източника и разпространяващ се със скорост c - както е на Фиг.1.
Нека смятаме, че зарядът източник е функция на своите координати и време (r',t').
Потенциалът - решение на Поасоновото уравнение би бил
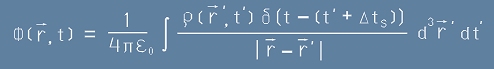 , [3]
, [3]
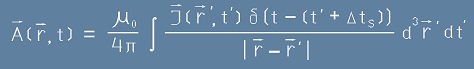 , [3.1]
, [3.1]
или използувайки свойството на делта-функцията в числителя
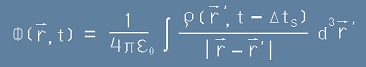 , [4]
, [4]
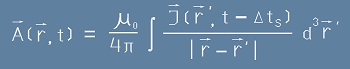 . [5]
. [5]
Последните две се наричат закъсняващи потенциали.
Аргументът време в числителя  показва закъснение -
показва закъснение -
те отразяват промяна в по-ранен момент, отколкото е временния аргумент t за наблюдателя в ляво.
коментари
Радостин Желязков 16.06.2011
________________________________________________________________________________________
учебни статии по физика
 Закъсняващи потенциали
Закъсняващи потенциали
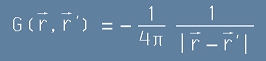 . [9p]
. [9p]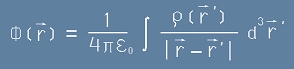 [10.1mp]
[10.1mp]
 [11.1mp]
[11.1mp] (виж Фиг.1).
(виж Фиг.1). на източника t' от времето, в което наблюдателя вижда полето t.
на източника t' от времето, в което наблюдателя вижда полето t. . [1]
. [1]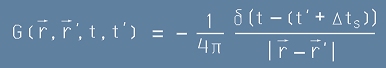 . [2]
. [2]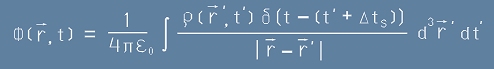 , [3]
, [3]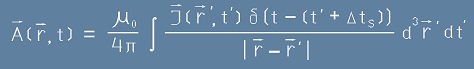 , [3.1]
, [3.1]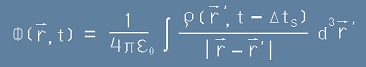 , [4]
, [4]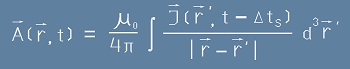 . [5]
. [5] показва закъснение -
показва закъснение -