 Гравитация
Гравитация
Този текст подпомага разбирането на Общата Теория на Относителността (ОТО).
Предните статии са:
Матрицата I,
Матрицата II,
Матрицата III,
Ковариантна производна на вектор,
Символи на Кристофел,
Теорема на Ричи,
Успоредно пренасяне,
Кривини,
Производна на Ли,
Геодезично отклонение,
Материя,
Уравнение на Поасон.
Гравитационно поле
В Нютонова механика, полето - сила, която действува на единична маса представлява градиент на потенциала:
 ,
където потенциалът Ф удовлетворява уравнението на Поасон (виж [9] от едноименната статия):
,
където потенциалът Ф удовлетворява уравнението на Поасон (виж [9] от едноименната статия):
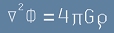 . [1]
. [1]
Това уравнение е подбрано, защото в дясната му страна стои плътност,
тоест то е удобно за отправна точка, ако трябва да направим аналогия с Тензора на Енергията - виж статията "Материя".
На това място Айнщаин, търсейки уравнението на полето, вече е имал предвид принципа за еквивалентност
между гравитацията и инерцията, както и идея, че около всяка маса възниква пространствена кривина - идентична с гравитационното привличане.
Да потърсим аналогия с уравнението [1].
В дясната страна, вместо плътност би трябвало да стои тензора на енергията, а в ляво - израз за пространствената кривина.
Тензорът на енергията има два индекса. Следователно в лявата страна трябва да участвува не Тензор на кривината на Риман - който е с четири индекса,
а Тензора на Ричи, който е точно с два. Ето как се поражда предположение (вероятно още у Айнщайн) за уравнение от вида:
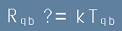 .
.
Но точно такова равенство щеше да има проблем със закона за запазване на енергията, който би изисквал условие
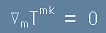 .
.
Затова Айнщайн конструира подходящ тензор, вече споменат в [5] от статията "Кривини":
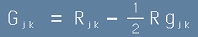 .
.
Така се е стигнало до известното
Уравнение на Айнщайн
 .
.
коментари
Радостин Желязков 12.03.2011 /корекция 11.02.2012/
________________________________________________________________________________________
учебни статии по физика
 Гравитация
Гравитация
 ,
където потенциалът Ф удовлетворява уравнението на Поасон (виж [9] от едноименната статия):
,
където потенциалът Ф удовлетворява уравнението на Поасон (виж [9] от едноименната статия):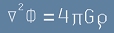 . [1]
. [1]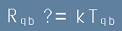 .
.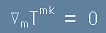 .
.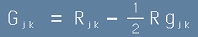 .
. .
.